共通テスト新課程数学IA｜図形と三角比の解き方と勉強方法

2024年12月17日2025年2月28日

2025年度（令和7年度）からの共通テストでは、数学IAの内容が新課程に対応し、大きく変わります。その中でも「図形と三角比」は、数学IAの中核を成す分野であり、図形問題や三角比を利用した計算問題が多く出題されることが予想されます。

新課程では、単なる公式の暗記だけではなく、「思考力・判断力・表現力」 が問われる問題が増加する傾向です。例えば、三角形における正弦定理・余弦定理の理解を前提としつつ、与えられた図形や条件から「何をどのように求めるか」を考える力が重要視されます。特に、複雑な図や複数の解法が考えられる問題では、苦手意識を持つ受験生が多い分野です。

多くの受験生が直面する課題としては、次のような点が挙げられます。

定義や公式が曖昧で、解法が思い浮かばない。
問題の図が複雑でイメージがつかめない。
計算過程でミスが多くなる。

「図形と三角比」は得意不得意が分かれやすい分野ですが、基礎をしっかり固め、問題に対するアプローチ方法を身につけることで、得点源に変えることが可能です。

本記事では、図形と三角比の勉強法や攻略のコツについて、具体的な解法や練習法を交えて解説します。苦手意識を克服し、共通テストで確実に点数を取るための第一歩を踏み出しましょう。

大学受験塾「ウィズスタディ」に相談

必見無料受験相談はこちら

リンク先 : https://jisyusidou.com

オンライン学習管理塾「ウィズスタディ」が無料学習相談を１対１で行っているので、上記ボタンから気軽にご応募ください。

図形と三角比が苦手になる原因

「図形と三角比」は数学IAの中でも多くの受験生が苦手意識を持つ分野です。
その主な原因は、定義や公式の理解不足や、複雑な図形を見た瞬間に解法が浮かばないことにあります。
ここでは、具体的な原因とその背景を解説します。

定義や公式の理解不足

「正弦定理」や「余弦定理」は、三角形の辺や角を求める際の必須ツールです。
しかし、以下のような問題に直面することが多いです。

公式を覚えているだけで、使い方がわからない。

問題のどの部分で正弦定理・余弦定理を使うべきか判断できない。

例えば、
「三角形の1辺の長さを求めよ」 という問題でも、公式を単に暗記しているだけでは対応できません。どの情報（角度・辺の関係）が与えられているのかを読み取り、適切な公式を選び取る力が求められます。

図形のイメージがつかめない

「図形と三角比」は、与えられた条件を正確に図に落とし込んで理解する力が重要です。
しかし、次のような課題に直面しがちです。

「図を描くのが面倒」「どのように補助線を引けば良いかわからない」

平面図形の問題で立体的なイメージがつかめない…

これにより、問題の途中で手が止まってしまうケースが多くなります。
特に「複雑な図形」や「条件が多い問題」では、図の書き方に工夫が必要です。
補助線や等積変形などの手法を知らないまま問題に取り組んでも、時間を浪費することになります。

計算過程でのミスが多い

図形問題や三角比の問題は、途中の計算量が多くなることがあります。
特に以下のミスが頻出します。

三角比（sin, cos, tan）の値を間違える
平方根や分数の計算ミスが起こる
式の変形ミスによって誤答になる

思考力を問う問題に対応できない

共通テストでは、単に公式を当てはめるだけでなく、与えられた条件から論理的に考える力が求められます。

例えば…

「補助線を引いて三角形の関係性を見つける」
「条件から別の三角形を使って解を導く」

といった「考えさせる問題」が多く出題されます。
しかし、これに対する演習量が不足していると、どこから手をつけるべきかわからず、解答が進みません。

図形と三角比の基本の確認（正弦定理の公式・余弦定理の公式）

「図形と三角比」を得意分野にするためには、まず基礎を固めることが重要です。公式の丸暗記ではなく、定義や使い方を正確に理解し、簡単な例題を通じてその使い方を身につけましょう。
ここでは、頻出のポイントと重要な基礎事項を整理します。

三角比（sin、cos、tan）の基本

三角比は「角度」と「辺の長さ」の関係を表す重要な概念です。
直角三角形において、以下の定義は必ず押さえましょう。

• 正弦（sin θ）：対辺 ÷ 斜辺

• 余弦（cos θ）：隣辺 ÷ 斜辺

• 正接（tan θ）：対辺 ÷ 隣辺

三角比のポイント

特殊角の値（30°, 45°, 60°） は必ず暗記する。
「tan θ = sin θ ÷ cos θ」の関係も理解する。

角度	sin θ	cos θ	tan θ
30°	1/2	√3/2	1/√3
45°	√2/2	√2/2	１
60°	√3/2	1/2	√3

三角比の基本例題

角度30°の直角三角形で、斜辺が10のとき、対辺の長さはどうなるかな？

「sin 30° = 1/2 → 対辺 = 10 × (1/2) = 5」になります！

正弦定理・余弦定理の使い方

三角形における辺や角を求める際、正弦定理と余弦定理は必須ツールです。

正弦定理の公式

条件：三角形の2つの角と1つの辺が分かっている場合に使う。

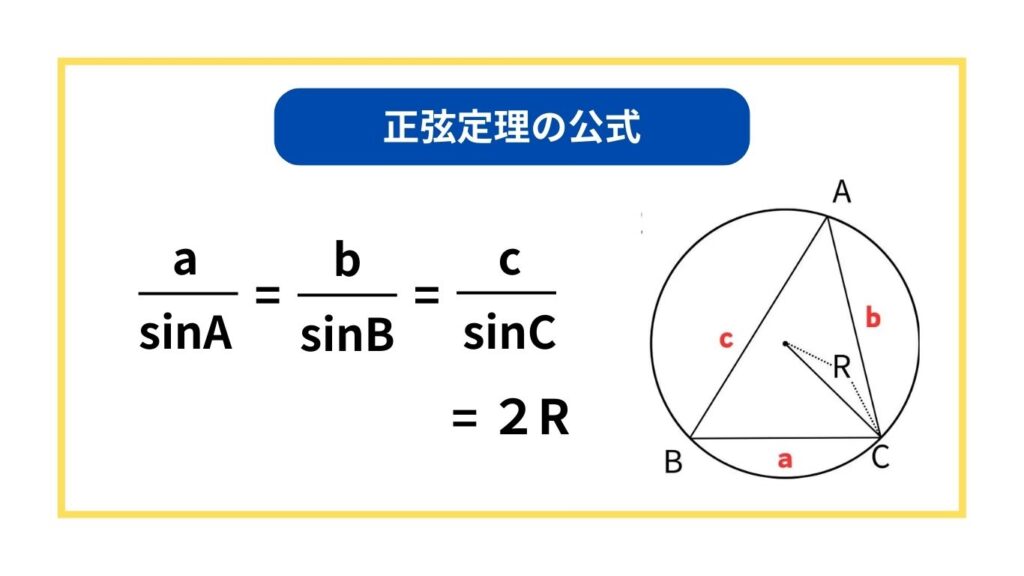
余弦定理の公式

条件：三角形の2辺とその間の角が分かっている場合に使う。

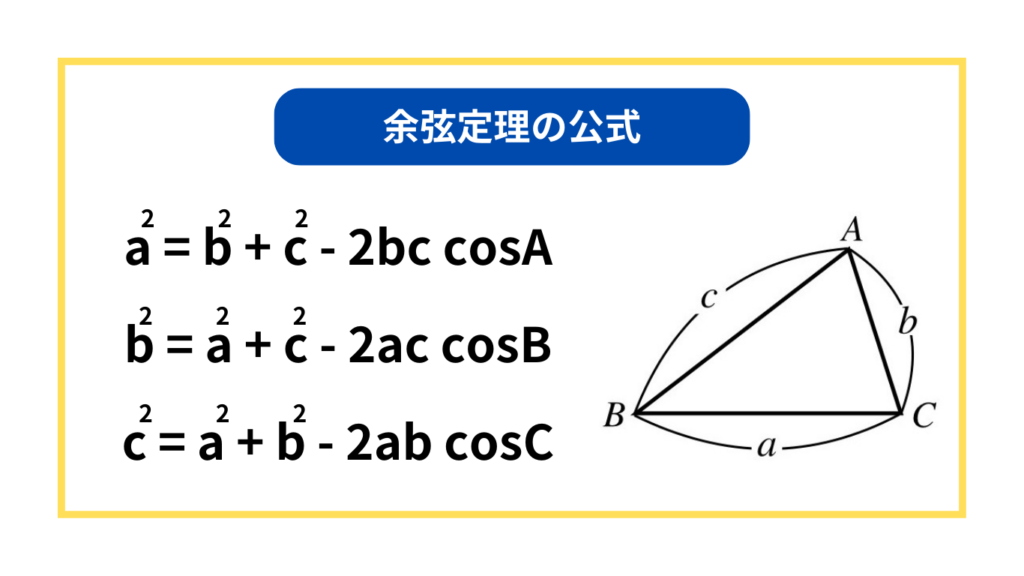
正弦定理・余弦定理のポイント

正弦定理は角度が与えられている問題に適用しやすい。
余弦定理は「辺の長さ」や「角度」が計算で求められる問題に対応する。

正弦定理・余弦定理の例題

三角形ABCにおいて、a = 6、b = 8、C = 60°のとき、辺cの長さを求めよ。

図形の基礎：補助線や相似の活用

平面図形問題では、補助線や相似の考え方が重要です。

補助線を引くコツ: 与えられた図形に足りない線を加えて、三角形や四角形の関係性を明確にする。
相似の活用: 三角形が相似である条件（角相似、辺の比）を押さえておく。

例題：「二等辺三角形に補助線を引くことで、直角三角形の比を使って辺の長さを求める」など。

補助線の使い方

「補助線」とは、元の図形にない線を追加して問題を解きやすくする手法です。
補助線を引くことで、次のような効果があります。

直角三角形を作る: 三角比を利用しやすくする。
三角比を利用しやすくする: 辺の比を利用できる。
面積や長さの関係を明確にする: 問題の条件を図で視覚化する。

補助線の引き方のコツ

STEP

三角形の高さを引く

二等辺三角形や正三角形の場合に有効。

STEP

対角線を引く

四角形を2つの三角形に分けることで解きやすくなる。

STEP

中点を通る線を引く

対称性を利用して図形の関係を明確にする。

例題と解法

例題：「二等辺三角形ABCにおいて、AB = AC, ∠A = 30° のとき、BCの長さを求めよ。」

解法：頂点Aから辺BCに高さを引くことで、直角三角形を2つ作る。
高さを「h」とすると、三角比を使って求められる。

相似の活用

「相似」は図形問題で頻出のテーマです。
三角形が相似である条件を理解しておくと、辺の長さや面積の比が求めやすくなります。

三角形が相似である条件

2つの角が等しい場合（角相似）
2辺の比が等しく、その間の角が等しい場合
3辺の比がすべて等しい場合

相似を利用するポイント

相似な三角形を見つけることで、辺の比から長さを求める。
面積比は辺の比の2乗になることを利用する。

例題と解法

例題：「高さが共通な台形において、上底と下底の比が2:3のとき、面積の比を求めよ。」

解法：・台形の中に補助線を引き、2つの相似な三角形に分ける。
・辺の比が2:3なら、面積の比は 2^2 : 3^2 = 4 : 9 となる。

「図形と三角比」基礎固めの勉強法

手を動かして図を描く練習をする

図を自分で書きながら、条件と公式を当てはめる習慣をつける。

基本例題を繰り返し解く

正弦定理・余弦定理の使い方が自然に身につくまで、簡単な問題を解き続ける。

間違えた問題は必ず振り返る

どの公式を使えばよかったのか、どの部分でつまずいたのかを分析する。

高校数学の基礎から学びたい方はこちらから

あわせて読みたい

高校数学が全くわからない人必見！基礎から学ぶ最強の勉強法と克服ステップ高校数学が全くわからない人に向けた勉強法を徹底解説！中学数学の復習から高校数学の基礎固め、効率的な学習法やモチベーション維持のコツまで、具体的な克服ステップを紹介します。

共通テスト対策｜攻略法と勉強のコツ

共通テストの「図形と三角比」では、問題文を素早く読み取り、解法の方向性を見つける力が求められます。
公式を当てはめるだけではなく、図形の特徴や条件を活用することで効率よく解ける問題が多いため、ここでは具体的な攻略法と勉強のコツを解説します。

解法の流れをつかむ

問題を解く際に最初に大切なのは、解法の方向性をつかむことです。
問題文を読み、与えられた条件を確認し、次のポイントを考えましょう。

問題文から「与えられている情報」を整理する

例：「角度が分かっている」「1辺の長さが与えられている」など。
→ 正弦定理や余弦定理を使う判断材料になる。

三角形の特徴や構成を考える

直角三角形か？
→ 三角比（sin、cos、tan）が使える。
2辺と角度が与えられているか？
→ 余弦定理を適用。
対角と辺の比を求める問題か？
→ 正弦定理が有効

補助線を引いて条件を明確にする

高さを引くことで直角三角形ができ、三角比が利用しやすくなる。
• 中点や角の二等分線を引いて対称性や相似を見つける。

「補助線を引く」「三角形の特徴を見つける」のテクニック

補助線の基本パターン（手順）

STEP

高さを引く

二等辺三角形や正三角形では高さを引いて左右の直角三角形に分けることで、三角比が活用できる。

STEP

角の二等分線を引く

与えられた角を半分に分けることで、相似な三角形や辺の比を利用しやすくなる。

STEP

対角線を引く

四角形の問題では対角線を引いて2つの三角形に分割し、三角比や相似の考え方を使う。

頻出パターン演習

共通テストの「図形と三角比」では、出題傾向がある程度決まっています。
過去の問題を分類し、次のパターンを重点的に演習しましょう。

パターン1：辺の長さや角度を求める問題

条件：「1つの角度と2辺の長さが与えられている。

解法：余弦定理を使い、残りの辺を求める。

パターン2：三角比の値を求める問題

条件：「特殊角（30°, 45°, 60°）や辺の比が与えられている。

解法：三角比の定義や特殊角の値を活用する。

パターン3：相似な三角形を利用する問題

条件：「補助線を引くことで三角形の相似が見つかる。

解法：相似条件を使い、辺の比や面積の比を求める。

「図形と三角比」練習法

問題文を見た瞬間に「何を求めるのか？」を考える習慣をつける。
「正弦定理」「余弦定理」「相似」のどれを使うべきかを意識しながら解く。
過去問や模試の問題をカテゴリ分けし、繰り返し解いてパターンを身につける。

図を使って視覚的に理解する

図形問題では「図を描く」ことが解法のカギです。
頭の中だけで解こうとせず、手を動かして図を描くことで次の効果があります。

条件が視覚化され、何を求めればよいかが明確になる。

補助線や三角形の特徴が見つけやすくなる。

作図から入る勉強法

問題を解く際、必ず「与えられた条件から図を描くこと」を徹底する。
自分で補助線を引き、どの部分に三角比や公式が使えるのかを確認する。

例題と解法

例題
「三角形ABCにおいて、AB = 5、AC = 7、∠A = 60°のとき、辺BCの長さを求めよ。」

解法

STEP

図を描き、与えられた条件を整理する。

STEP

余弦定理を使ってBCを求める

STEP

計算して答えを導く

共通テストに役立つ情報はこちらから

あわせて読みたい

共通テストは何点必要？大学別の得点率・合格ライン・最低点を徹底解説【共通テストで志望校合格！】難関国公立〜中堅私立まで大学ランク別の得点目安を解説。模試や過去問を活用した効率的な勉強法で得点率をアップし、最適な受験戦略を立てよう！

あわせて読みたい

共通テスト直前1週間の勉強法｜効率的に得点を伸ばす最後の対策共通テスト直前1週間の効率的な勉強法を徹底解説！時間の使い方や科目別対策、モチベーション維持のポイントを具体的に紹介します。得点力を最大限に引き上げ、志望校合格を目指しましょう！

「図形と三角比」におすすめの勉強法と教材

「図形と三角比」を得意分野に変えるためには、適切な教材選びと効率的な勉強法が重要です。
苦手意識が強い分野でも、「基本→実践→確認」の流れを繰り返し、必要に応じてスマホやオンラインツールを活用することで、着実に得点源にすることができます。ここでは具体的な勉強法とおすすめの教材を紹介します。

おすすめの教材：図形と三角比が得意になる参考書・問題集

① 基礎固め向け教材

『チャート式基礎からの数学IA』（数研出版）

解法が丁寧に説明されているので、公式の使い方や問題のアプローチ方法を一から学べます。
「例題→練習問題」の構成で、理解度を高めながら進められる点がポイント。

『学校で習ったことがちゃんとわかる数学IA』（旺文社）

高校数学が苦手な人向けの優しい解説書。図形問題も視覚的に説明されており、直感的に理解しやすい。

② 問題演習向け教材

『Focus Gold 数学IA』（啓林館）

難易度別に問題が整理されており、標準問題から入試レベルまで段階的に力をつけることが可能です。
解答解説が丁寧で、複雑な図形や三角比の問題にも対応。

『共通テスト数学IA 実戦問題集』（河合出版／駿台文庫）

https://www.sundaibunko.jp/contents/book/1233

共通テスト特有の問題形式に慣れるための良質な問題が収録されています。
図形と三角比の頻出パターンを徹底的に演習できるのが魅力です。

③ 問題パターンを確認する教材

『数学基礎問題精講IA』（旺文社）

図形と三角比の典型問題を効率よく学べます。解説がシンプルでわかりやすい。
時間をかけずにパターンを覚えたい人におすすめ。

スマホやオンラインツールを活用した理解促進

図形問題や三角比は視覚的な理解が重要です。苦手意識が強い人は、スマホアプリや動画教材を活用しましょう。

スタディサプリ

高校数学IAの講義動画が充実しており、図形と三角比の基礎から応用まで学べる。
短時間の講義なので、スキマ時間にも活用しやすい。

「Try IT（トライイット）」

無料動画教材で、図形の作図や補助線の引き方を視覚的に学ぶことができる。
特に苦手な部分は何度も動画を見返すことで理解が深まる。

スマホアプリ「数学トレーニング」

三角比や図形問題の解法を短時間で反復練習できるアプリ。
問題の種類が豊富で、パターン学習にも最適。

オンライン自習室・塾の活用

苦手な部分は塾やオンライン指導で質問し、理解の抜け漏れを防ぐ。
「無料オンライン自習室」を希望の場合は、以下のボタンからお問い合わせください。

無料オンライン自習室はこちら

無料で使えるオススメのオンライン自習室はこちらから

あわせて読みたい

近くに自習室がない方必見！無料で使えるオンライン自習室5選と活用術近くに自習室がなくても安心！無料で使えるオンライン自習室5選を詳しく紹介。高校生に向けた集中力を高める活用方法や、効率的に勉強を進めるコツも解説。自宅で学習環境を整えよう！

まとめ：「図形と三角比」の攻略法と勉強方法

「図形と三角比」の共通テスト対策では、解法の方向性を素早く判断し、補助線や相似を効果的に活用することがポイントです。
問題文を図で視覚化する習慣をつけ、頻出パターンの問題を繰り返し練習することで、本番でも落ち着いて解くことができるようになります。

また、「図形と三角比」を得意分野にするためには、基礎から始めて段階的に学習し、頻出パターン問題を繰り返し解くことが重要です。
動画教材やスマホアプリを活用して視覚的に理解することで、苦手意識を克服しやすくなります。
適切な教材と勉強法を組み合わせて、共通テストで得点源にできるよう着実に実力をつけていきましょう。